核心思想

一些定义

 树链剖分，简称树剖 树分 全称树学分析，是一个基于树形结构和线段树的启发式算法。其核心思想是把一颗树剖分为若干条链条，每段链条独自内部线性连续，然后利用以上特性结合更复杂的数据结构进行维护。

 本文介绍的属于 “重链剖分”。其可以用来解决修改树上两点之间路径上每个点的权值、修改子树中每个点权值、以及在线查询以上两种权值的和/最大值等问题。

 重链剖分的基本性质是: 对于树上每个节点，额外记录哪一颗子树的节点最多(最重)，将这颗子树的根节点记录为重儿子，即节点数最多的子树的根节点为重儿子。特别的，若一个节点有多个子树拥有最多的节点，那么随机选取其中一个的根节点作为重儿子即可。

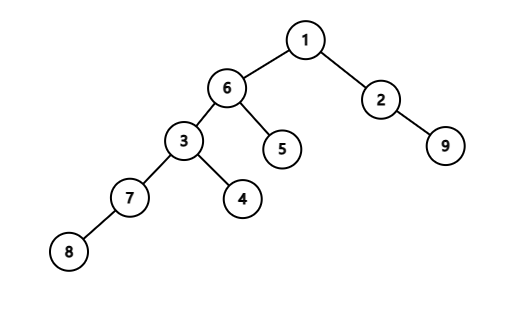
 如下图:

 图中，我们能很直观的看出，节点1的重儿子就是6，节点2的重儿子是9，节点3的重儿子就是7。”重”的定义是与我们的直观完全符合的。

 我们再定义重边是子节点是重儿子的边，反之则为轻边。同样是上面这张图，图中，1-6,6-3,3-7,7-8,2-9便是重边，而其他都属于轻边。我们再称重边连成的链条为重链。如上图，重链就是1-6-3-7-8 和 2-9。特别的，我们认为4、5这样不与任何重边相连接的点，本身构成重链，即 4 和 5 也是重链。容易看出，重链之间由轻边连接，即重链必定为一条链，不会有分叉；且树上每个点属于且仅属于一条重链。

 在维护的时候，我们的核心思路就是在重链上一次性更新尽可能多的节点，因为在轻边上我们一次更新的节点数很少。根据这样的性质，我们应当将树上的节点重新编号，并且把重链上的节点编号连续化，以便于区间维护。因此，我们将用 dfs 时的先后顺序来为作为新编号 (记为dfn) ，在dfs的时候先走重儿子，再遍历其他子树，使得重链上的 dfn 必然是连续的。

一些性质

 考虑重链剖分的基本性质: 节点数最多的子树的根节点为重儿子。我们从整棵树的根节点出发向下走，走到一个目标节点。如果走重链，那么我们一次走到不能再走重边为止；如果走轻边，那么前往的子树的大小不会超过当前树大小的一半(重链剖分的性质)，只会走一次。因此，我们总是在”走重链”和”走轻边”之间切换，而假设树有 $n$ 个节点，因为轻边的子树节点数不超过当前树的节点数的一半，所以我们走轻边的次数不会超过 $\log_2n$ 次，走重链的次数不会超过 $\log_2n + 1$ 次(因为轻-重交替)。因此，对于树上任意路径，轻边和重链的总数不会超过 $O(\log n)$ 数量级。

 再回到我们之前的 dfs 的方式，我们通过先访问重儿子使得重链上 dfn 连续，同时又由 dfs 的基本性质，在结束访问一个节点前，需要结束访问其子树上所有的节点。因此，对于一个 dfs 序为 dfn 的点，若其子树(包括自己这个节点)大小为size，则其和其子树的编号，正好覆盖 [dfn,dfn + size -1] 这个整数区间，即 子树的 dfn 连续。

具体实现

 首先，我们往往根据情况需要一个维护连续区间，支持区间查询的数据结构。一般来说，我们会对应选用 树状数组/线段树/分块 等数据结构来维护。为简化讨论，本文将统一使用线段树作为维护区间的数据结构。大致如下:

1
2
const int N = 1e5 + 3; // 视题目而变
dark::segment_tree <int,N> t; // 线段树

 其次，我们要通过 dfs 处理出一些关键的信息，而大部分情况下，需要两次dfs。具体维护的信息请看代码注释:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
/* 注: 本文节点编号 1-base */
vector <int> g[N]; // 用 vector 存图
int son[N];     // 重儿子节点，必须维护
int top[N];     // 重链最顶部的节点，必须维护
int fat[N];     // 父亲节点，必须维护
int siz[N];     // 子树大小，必须维护
int dep[N];     // 节点深度，有需要就维护
int dfn[N];     // dfs 序，必须维护
int rev[N];     /*
    dfn 的反函数(reverse)，即满足:
    dfn[rev[i]] = rev[dfn[i]] = i;
    在有节点初始权值即线段树需要build的时候，才需要维护
*/

// 处理出 son,fat,siz,dep信息
void dfs1(int u) { // u 为当前节点
    int maxsiz = -1; // 当前节点最大的子树大小
    siz[u] = 1;      // 至少包含当前节点的 siz
    for(int v : g[u]) { // C++11特性。此处用来遍历 u 所有边，v为指向的点
        if(v == fat[u]) continue; // 父节点不重复遍历
        dep[v] = dep[u] + 1;
        fat[v] = u;
        dfs1(v);
        siz[u] += siz[v];
        if(siz[v] > maxsiz) {
            maxsiz = siz[v];
            son[u] = v;
        }
    }
}
int CNT = 0; // dfn的总数
// 处理出 top,dfn,rev
void dfs2(int u,int tp) { // u 同上，tp为当前重链顶部
    dfn[u] = ++CNT;
    rev[CNT] = u;
    top[u] = tp;
    if(!son[u]) return; // 没有重儿子 = 没有儿子
    dfs2(son[u],tp);    // 先走重儿子
    for(int v : g[u]) { // 同上
        // 重儿子走过了，父节点不走
        if(v == fat[u] || v == son[u]) continue; 
        dfs2(v,v);      // 走轻边，top改变
    }
}


应用场景

在线求最近公共祖先(LCA问题)

 具体思路类似倍增求 LCA (如果你还不知道LCA以及其倍增解法，点击这里)，同样是从两个底部节点往上(根节点)跳寻找第一处祖先相同的地方。不同的是，在重链剖分的情况下，我们向上跳操作，走的是重链和轻边。假设当前有两个节点为 x 和 y，通过交换操作我们保证 dep[top[x]] 不超过 dep[top[y]] ，如果 top[x] 和 top[y] 不相等，说明 LCA 在必定在 top[x] 所在节点的上方，我们将 x 更新为 fat[top[x]]，重复以上操作，直到 top[x] = top[y]。此时，x、y已经在同一条重链上，由 LCA 的知识易知，LCA就是 x 和 y 中深度更浅的那个点。

1
2
3
4
5
6
7
8
9
int getLCA(int x,int y) {
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]]) 
            y = fat[top[y]];
        else
            x = fat[top[x]];
    }
    return dep[x] < dep[y] ? y : x;
}

 该实现只需要 $O(n)$ 的预处理时间，以及 $O(\log n)$ 的单次查询时间，优于倍增法 $O(n\log n)$ 的预处理时间。而且，一般除了满二叉树、一直走轻边的情况，单次查询很难跑满 $ \log_2 n$ 的 “跳top” 上限次数，实际常数比较小。

维护路径和子树权值

 对于查询路径，重链剖分可以将其转化为一个区间维护问题。例题 Luogu3384:

题目描述

如题，已知一棵包含 $N$ 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

  • 1 x y z，表示将树从 $x$ 到 $y$ 结点最短路径上所有节点的值都加上 $z$。

  • 2 x y，表示求树从 $x$ 到 $y$ 结点最短路径上所有节点的值之和。

  • 3 x z，表示将以 $x$ 为根节点的子树内所有节点值都加上 $z$。

  • 4 x 表示求以 $x$ 为根节点的子树内所有节点值之和

分析

 前两个操作其实就是区间修改 + 查询路径权值和。通过树剖，我们可以将其划分为轻边和重链。类似前面求 LCA 的方法，我们在修改的时候依然使用向上跳的方式修改，对于每一次从 x 跳到 top[x] 再变为 fat[top[x]]，其 dfn 是连续的。因此，我们可以直接在线段树上修改这一段连续区间。最后，如果 x 已经跳到了 LCA 这个点，x、y已经在一条重链上时，只需再把 dfn[x] 到 dfn[y] 这一段修改了即可。查询同理。此时，单次操作时间复杂度为 $O(\log^2 n)$。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
dark::segment_tree <int,N> t; // 线段树

void addPath(int x,int y,int val) {
    while(top[x] != top[y]) {
        if(dep[top[x]] < dep[top[y]]) swap(x,y);
        t.add(dfn[top[x]],dfn[x],val); // 区间加 
        x = fat[top[x]];
    } /* 现在 top[x] == top[y] */
    if(dep[x] > dep[y]) swap(x,y);
    t.add(dfn[x],dfn[y],val);
}


// 类似，此处略去
int sumPath(int x,int y);

 后面两个操作则是关于子树信息的维护。由于树剖以后，子树内部 dfn 连续，因此修改子树信息只需一次区间操作即可。单次操作时间复杂度为 $O(\log n)$

1
2
3
4
5
6
7
8
9

void addTree(int x,int val) {
    t.add(dfn[x],dfn[x] + siz[x] - 1,val);
}

int sumTree(int x) {
    return t.sum(dfn[x],dfn[x] + siz[x] - 1);
}

 综上，经过了 $q$ 次操作以后，该程序的总时间复杂度为 $O(n + q\log^2 n) $。而事实上由于树剖本身常数小，其跑起来像是少了一个 log 一样(但是可以被满二叉树卡满)。

结语

 重链剖分是一种独特的数据结构，其通过启发式的划分轻重链并重新编号，使得重链上编号连续，进而将树上路径问题和子树问题问题转化为区间维护问题。其本体核心在于两次 dfs 以及跳 top 的一个过程。事实上写多了重链剖分，你就会发现大部分这方面的基础题主要考察如何转化模型为树剖，以及如何设计内部维护的数据结构(比如线段树、分块等等)。如果想做更多的题目巩固可以参考下 OIwiki 给出的练习 or Conless 的学习计划: